病态观测方程广泛存在于大地测量和遥感解算模型中，如GNSS快速定位，卫星重力反演、InSAR相位解缠以及植被参数反演等。Tikhonov和TSVD（Truncated Singular Value Decomposition）正则化是处理病态模型的两种著名方法。Tikhonov正则化是在最小二乘准则的基础上对参数施加二范约束，并利用正则化参数调节二者的平衡；TSVD正则化则通过截掉系数矩阵的小奇异值避免放大高频观测误差对参数估值的影响，仅利用大的奇异值及相应的特征向量构建参数估值。对于Tikhonov正则化，给定一个正则化参数，其低频部分往往过度正则化，而高频部分则欠正则化；对于TSVD正则化，其中频部分无法得到有效处理。

课题组根据正则化解的精度最优（MSE最小）准则，建立了自适应正则化估计理论，确定不需要正则化的低频部分，需要截断的高频部分以及需要正则化处理的中频部分，改善了传统正则化解的精度。图1和图2为采用第一类积分方程比较各种正则化解的MSE（OTikO:普通Tikhonov正则化，PTikO: 仅低频部分不正则化，Inada:自适应正则化解（不迭代），ITada：自适应正则化解（迭代），OTsvd: TSVD正则化）。显然，自适应正则化解的精度显著优于传统方法。

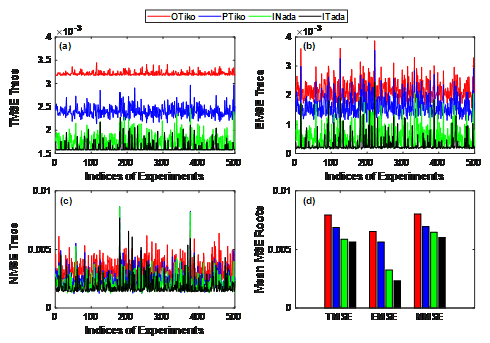
Fig.1 MSEs of OTiko solution, PTiko solution, INada solution and ITada solution over 500 simulations.

(a): TMSE (b): EMSE (c): NMSE (d): The means of MSE roots

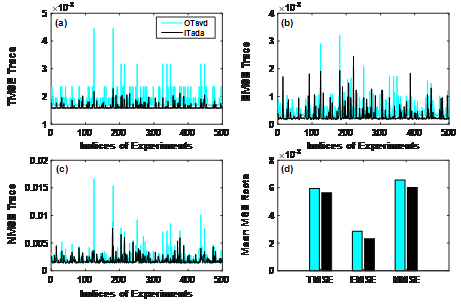
Fig.2 MSEs of OTsvd solution and ITada solution over 500 simulations.

(a): TMSE (b): EMSE (c): NMSE (d): The means of MSE roots over 500 simulations

该研究成果发表于地球科学和遥感领域知名期刊《IEEE TGRS》，研究工作获得了国家自然科学基金项目（41974002和42192532）的资助。

论文引用：

Ji, K., Shen, Y., Chen, Q., Li, B., & Wang, W. (2022). An Adaptive Regularized Solution to Inverse Ill-Posed Models. IEEE Transactions on Geoscience and Remote Sensing, 60, 1-15.